Essa postagem é um complemento das postagens sobre equações do 1º e 2º grau (clique sobre os números se você ainda não as leu)
Nas nossas contas até o momento, sempre que resolvíamos alguma operação colocávamos um símbolo antes das respostas. Esse símbolo é o da igualdade (ou igual : ' = ').
Usávamos a igualdade para casos como por exemplo: 3 x 2 = 6
Nesses casos e em outros semelhantes, temos uma operação de um lado e o valor dessa operação do outro. Em equações os casos vão ficar um pouco diferentes. Passaremos a encontrar casos onde temos operações matemáticas de um lado e também do outro.
Inicialmente, pensem em: 3 x 2 = 6 x 1 . Percebam que se resolvermos separadamente cada lado da igualdade, vamos encontrar o mesmo resultado (3 x 2 = 6 ; 6 x 1 = 6).
Essa é a ideia básica da igualdade, os dois lados são IGUAIS (Valores iguais)
Mas uma igualdade como essa que eu demonstrei, não serve para nada, afinal poderíamos ter resolvido separadamente como eu disse. De agora em diante, as operações passarão a depender umas das outras. Para isso precisamos aprender como trabalhar ao mesmo tempo com os dois lados da igualdade, como se fosse um só.
Para isso precisamos aprender o que acontece com a operações matemáticas básicas em igualdades.
Soma
Vamos fazendo e entendendo ao mesmo tempo:


Colocaremos todos os termos em um mesmo lado da igualdade.
Para isso vamos primeiramente escolher um lado. Por conveniência, vamos escolher o da esquerda (mas tanto faz).
Agora, no lado direito temos 4 e um 1. Vamos passar eles para o outro lado.
Ao fazer isso, o sinal se inverte, tínhamos um 4, agora teremos um -4 e quanto ao 1 tínhamos um +1 e agora vamos ter do outro lado um -1:
Para isso vamos primeiramente escolher um lado. Por conveniência, vamos escolher o da esquerda (mas tanto faz).
Agora, no lado direito temos 4 e um 1. Vamos passar eles para o outro lado.
Ao fazer isso, o sinal se inverte, tínhamos um 4, agora teremos um -4 e quanto ao 1 tínhamos um +1 e agora vamos ter do outro lado um -1:

Notem que ao fazer isso, deixamos o lado direito da igualdade sem nada, sempre que fizermos isso temos que colocar um zero no lado que não sobrou nada.


Agora que vimos a soma, podemos generalizar .
Toda vez que passamos um número para o outro lado, a operação é invertida. Afinal, era soma e virou subtração.
Toda vez que passamos um número para o outro lado, a operação é invertida. Afinal, era soma e virou subtração.
Vejam em um exemplo de cada abaixo.
Subtração

Multiplicação
A direita da igualdade tínhamos 2 x 1, ao passar para a esquerda, eu podia escolher o 2 ou o 1.
Escolhi o 1 primeiro. Por isso ficou 2 dividido por 1, dando como resultado final 2 =2
Para facilitar, pense "no lado direito, estava multiplicando 1, por isso eu passo dividindo o 1 para o outro lado"
Eu podia também escolher passar o 2, por isso ficou 2 dividido por 2, dando como resultado final 1 = 1.
Divisão
Raízes
É valido para qualquer raiz, se fosse raiz cúbica, no outro lado seria elevado ao cubo.
* Várias vezes durante a postagem eu disse "passar para o outro lado". Esse conceito na verdade não existe. Muitos professores são contra esse termo 'passar', inclusive. Entretanto, muitos alunos já aprenderam com esse nome, e, com ele realmente é mais fácil de se aprender, porque realmente parece que foi isso que aconteceu mesmo.
Tínhamos um + de um lado e ele simplesmente desaparece e foi para o outro lado como um - , é natural dizer que ele passou para o lado de lá.
Tínhamos um + de um lado e ele simplesmente desaparece e foi para o outro lado como um - , é natural dizer que ele passou para o lado de lá.
Mas, vamos aprender agora o que realmente acontece.
Porém, notem que é apenas como aprofundamento do conteúdo, não vai alterar em nada a resolução de problemas e você ainda pode continuar falando 'passa para o outro lado' depois de aprender.
Assim como aprendemos em uma divisão, onde alterar o denominador e o numerador ao mesmo tempo não altera o resultado, em uma igualdade também acontece isso. Vejamos:
3 + 1 = 1 + 3
Em um lado, temos 3 + 1 = 4. Do outro 1 + 3 = 4. Ambos deram resultados iguais. Agora, vamos multiplicar os dois lados da igualdade por 2.
2 x (3 + 1) = 2 x (1 + 3)
(6 + 2 ) = ( 2 + 6 )
8 = 8
Viram que a igualdade ainda se mantém.
Entretanto, antes a igualdade era 4 = 4, agora é 8 = 8.
Percebam que as igualdades nesse caso, são uma o dobro da outra. Justamente porque multiplicamos ambos os lados da igualdade por 2.
O principio está provado, não importa o que aconteça com um lado da igualdade, se eu fizer com o outro então a igualdade sempre se manterá.
Entretanto, antes a igualdade era 4 = 4, agora é 8 = 8.
Percebam que as igualdades nesse caso, são uma o dobro da outra. Justamente porque multiplicamos ambos os lados da igualdade por 2.
O principio está provado, não importa o que aconteça com um lado da igualdade, se eu fizer com o outro então a igualdade sempre se manterá.
Vamos ver então naqueles casos que aprendemos mais em cima, o que realmente acontece. Tínhamos que:
Percebam que posso alterar como quiser um lado da igualdade, desde que faça o mesmo com o outro. Assim sendo, colocaremos um -4 e um - 1 no lado à direita da igualdade:
Para que isso possa acontecer, tenho que colocar um -4 e -1 do lado também.

E agora, vamos resolver somente o primeiro lado em que alteramos, o lado à direita igualdade:

Comparem com o primeiro exemplo que vimos, lá em cima, e vejam que ficou exatamente igual!
Só para concluir, vamos ao ultimo exemplo:

Temos uma raiz quadrada à esquerda da igualdade, vamos então, elevar ao quadrado.

Não esquecendo que temos de fazer o mesmo à direita da igualdade:

Agora resolvemos somente onde alteramos primeiro:

Dessa forma, fica comprovado a hipótese levantada mais acima, que a igualdade não se altera se alterarmos seus dois lados simultaneamente.


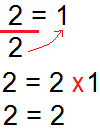




Nenhum comentário:
Postar um comentário
Gostou da Postagem ou ficou com alguma duvida? Coloque aqui sua sugestão, dúvida ou agradecimento pela postagem.
Lembre-se:
* Qualquer comentário considerado ofensivo ou inadequado será imediatamente excluído!
*Não divulgue outros blogs ou páginas nos comentários
Edson