Multiplicação - Divisão

Multiplicação

A operação de multiplicar um número por outro consiste, na verdade, a uma sequência de somas do primeiro número.

Então, simplificadamente, multiplicação é uma SOMA.

Multiplicar 2 x 3 . Na verdade é somar +3 duas vezes. Assim : +3+3 = 6.

Multiplicação também uma operação comutativa, ou seja,  A ordem dos fatores não altera o resultado .  2 x 3 = 3 x 2.

Pois, assim :  +2+2+2 = 6 .

Se parecer estranho +3 +3, imaginem que tem um '0' no começo de cada operação, assim 

0+3+3

Embora eu tenha dito que o resultado da operação é igual nos dois casos apresentados acima (justificando a comutatividade deles), não podemos afirmar que as operações são iguais, na verdade 

 2 x 3 é diferente de 3 x 2  .

A resposta para essa situação curiosa da multiplicação, é explicado usando a soma. Foi escrito acima que 2 x 3 = +3 + 3  (6), enquanto que 3 x 2 = +2 +2 +2   (6) . 

Ambos os resultados deram '6', mas as contas são diferentes. Acompanhe:
2 x 3: Vamos começar pela leitura da operação  "duas vezes três"

Isso significa que vamos pegar duas vezes o número '3'.
Já 3 x 2: "três vezes dois"

Isso significa que vamos pegar três vezes o número '2'  

Para efeitos de cálculo de maneira geral, em que somente a resposta importa, tanto faz o método, mas agora já sabemos qual é a maneira certa de fazer.


Agora, se multiplicar é somar um número a ele mesmo várias vezes, podemos sempre fazer isso manualmente, somando. 

3 x 5 = +5 +5 +5  = 15
4 x 6 = +6 +6 +6 +6 = 24
2 x 9 = +9 +9 = 18
1 x 7 = 7    = 7

Mas e quando encontramos uma operação que é extremamente grande.
Exemplo: 35 x 19 

Poderíamos sim somar o 19 com o 19 trinta e cinco vezes, mas isso daria um trabalho imenso, imaginem:

+19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19 +19

Além de dar muito trabalho ter que escrever essa conta, isso não ajuda a resolver o problema, eu ainda teria que somar manualmente todas as vezes, correndo um risco imenso de errar.

Para multiplicações desse tamanho, ou ainda maiores, usaremos um mecanismo de multiplicação.

Vamos escrever os números um em cima do outro, com um 'x' (simbolizando multiplicação) :

Sempre começamos pelo número que está em baixo. Nele, vamos por partes da direita para a esquerda.

Então, primeiro o 9:

Multiplicaremos esse valor pelo número que está em cima, também começando da direita e indo para a esquerda, que no caso é o '5', assim:

9 x 5 = 45  . Da mesma maneira que aprendemos na soma, vamos colocar a unidade (5) em baixo da barra e vamos jogar a dezena (4) para a casa da dezena:


Agora que multiplicamos o 9 por 5, vamos seguir a ordem e multiplicar pelo 3, e após multiplicar vamos somar com o número '4' vermelho que está em cima do 3.

Fica:
9 x 3 = 27  ->  27 + 4 = 31 

Agora como não há mais nenhum número a esquerda do nosso 35, podemos simplesmente copiar o resultado em baixo da barra.

Pronto, fizemos as operações com o '9' . Resta fazer com o '1'. Antes, vamos colocar um sinal de "+" logo abaixo do nosso primeiro número vermelho embaixo da barra:

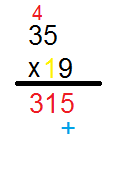
Vamos multiplicar então, o número 1 por 5 e depois por 3
Assim 1 x 5 = 5

Percebam que não coloquei o número embaixo do primeiro número em vermelho, coloquei depois do "+" e é, exatamente, assim que deve ser feito.

Multiplicaremos 1 x 3 = 3 e colocaremos no mecanismo

Agora, encontramos uma soma entre as barras, vamos então somar.

Percebam que não tem nada embaixo do 5 (do número 315), por isso, ele apenas foi repetido em baixo.

Por quê foi necessário colocar aquele "+" na segunda linha? 

Porque nesse mecanismo fazemos a multiplicação por partes, sendo que multiplicamos  primeiro a unidade e depois somamos com a multiplicação da dezena.

Ou seja, no exemplo, multiplicamos   9 x 35 e depois depois, multiplicamos 1 x 35 porém devemos lembrar que esse '1' é uma dezena, portanto ele não é um '1' e sim um '10'  . Na verdade nossa conta foi feita assim:

9   x 35 = 315
10 x 35 = 350  +
             ----------
             = 665

Então, aquele '+' do mecanismo, na verdade representa o número zero, que foi ocultado.

Veja outros exemplos:



 


Como multiplicar quando um número termina em zero?

Não muda muita coisa, apenas facilita nossa conta, veja:

1º Vamos contar os '0' dos números.
Nesse caso, temos dois '0' (um do número 30 e outro do 10). Assim sendo, vamos colocar 2 zeros em baixo da barra e depois vamos ignorar os '0's que estão em cima da barra:

Agora ficou muito fácil, multiplicaremos 1 x 3 e colocaremos a frente dos zeros:

Pronto, definimos, então, que sempre que tivermos zeros, basta colocá-los embaixo da barra e fazer a conta sem eles.



Divisão

Podemos pensar em dividir como uma separação de pedaços iguais.

Por exemplo, ao dividirmos uma maçã com duas pessoas, cortamos ela ao meio, obtendo assim duas partes iguais.

Nesse exemplo dizemos matematicamente que 1 maçã dividida por 2 pessoas, é igual a meia maçã para cada pessoa.

Esse é o princípio básico da divisão, dividir algo em outras partes iguais.

O símbolo da divisão é a barra ' / ' , ou os dois pontos '  :  ' , ainda pode ser representado pela barra das frações.

Usamos divisão desde sempre em nossas vidas, por isso muitas são fáceis de fazer. Dividir números por 2 ou por 3 são quase automáticas na nossa cabeça. Mas, existe uma maneira de fazer essas contas manualmente, essas e todos os outros casos mais difíceis. Encontramos o resultado da divisão usando outro mecanismo.

Exemplo: 45 / 5

O mecanismo consiste em colocar o número que queremos dividir a esquerda e o número pelo qual dividiremos a direita.

Agora, nos lembramos da tabuada: Qual número, de 1 a 9, que multiplicado por 5 é 45?

Pela tabuada, sabemos que: 5 x 9 = 45

Achamos nosso valor, então vamos colocar o 9 em baixo da barra

Multiplicaremos novamente, 5 x 9 e o valor encontrado colocaremos em baixo do 45 com um sinal de negativo (-):

Então, somaremos os dois valores a esquerda. (detalhe: Vamos somar os números da esquerda, mas lembrando que como o segundo '45' tem um sinal negativo, ao somar +45 com -45, encontraremos 0 como resposta, isso porque somar números com sinal oposto, é a mesma coisa que subtraí-los.

 Antes de prosseguirmos, vamos para a nomenclatura dos termos nesses mecanismo:

Esses nomes nos ajudam a criar uma equação para achar a Prova Real (Leia a postagem, clicando no link).

A equação é a seguinte:

Resultado x Divisor + Resto = Dividendo.

Vamos testar:

       9          x       5     +    0     = ?
                                                                      = 45

*Não se esqueçam, da prioridade das operação, primeiro multiplicamos o Divisor pelo resultado, e somente depois somamos com o resto (Se ainda não viu sobre o assunto, clique aqui).
Agora que sabemos os nomes, continuaremos.

 
E quando o dividendo for maior que nove vezes o divisor?

Para entender melhor sobre o assunto, veremos no exemplo.

Nesse caso faremos uma divisão por partes.

Exemplo: 66 : 3

Se pensarmos na tabuada do 3 temos:

3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
3 x 5 = 15
3 x 6 = 18
3 x 7 = 21
3 x 8 = 24
3 x 9 = 27

Nenhum valor se aproxima de 66.

Nesses casos, separamos o dividendo, pegando apenas um número. Ao invés de 66, vamos pegar somente o termo da esquerda, nesse caso, o 6.

Voltamos ao passo anterior: Existe um valor que multiplicado por 3 é igual a 6?
- Sim, vimos na tabuada que 3 x 2 = 6


Então, vamos colocar 2 no resultado e prosseguir da maneira que vimos anteriormente:

Vamos somar 6 - 6, cujo resultado é 0. Colocaremos, então, esse '0' em baixo da barra

Não podemos dividir o zero encontrado com o 3 do divisor. Então, terminamos essa parte. Partiremos agora para o número que ainda resta.

No começo dessa divisão, deixamos uma parte do número de lado, agora é a hora voltar para essa parte e continuar a conta:

Temos novamente 6 dividido por 3, então já sabemos que número colocar no resultado, o mesmo '2' tal como antes.

Faremos a multiplicação de 2 x 3 = 6 e colocaremos esse 6 encontrado em baixo do 06 que temos, assim:

Agora, somamos o 06 - 6. E encontraremos 00 de resto, ou seja, nossa conta terminou.

Também poderíamos, ao invés de usar esse mecanismo, fazer a tabuada do 3 até encontrarmos o 66. Descobrimos através do mecanismo que 3 x 22 = 66, então, eventualmente acharíamos esse valor se continuássemos a tabuada.

O problema é que fazer a tabuada pode ser algo muito cansativo, especialmente se fosse um número extremamente grande, como, por exemplo, se fosse 300 / 3. Poderíamos fazer a tabuada do 3 até encontrar o valor 300, que sabemos que é 3 x 100. 

Isso quer dizer que nossa tabuada teria 100 linhas. Extremamente demorado, ainda mais porque não necessário.

E se o resto da divisão não for zero?

Nesse caso, apenas algumas coisas vão mudar, veremos um exemplo já no mecanismo:

Vou fazer direto, pois, é igual.

Encontramos 1 de resto e não podemos mais dividir 1 por 2, porque 1 é menor que 2 ( ou matematicamente falando, 1 < 2). 

Esse é um critério de parada do divisão, podemos fazer a divisão até que seja encontrado zero no resto ou que o resto seja menor do que o divisor.

Nesse caso, podemos continuar de duas maneiras. A primeira é não continuar, paramos aqui mesmo dizendo que essa divisão não é exata, pois realmente ela não é. 

Ou podemos continuar dividindo, mas então, descobriremos um número fracionado.

Vamos fazer o fracionado.

Para isso, colocaremos uma vírgula ( , ) no resultado e colocaremos um zero (0) a direita do resto, assim:

Percebam que agora, podemos continuar nossa divisão, afinal 10 é maior que 2. Então, continuamos.

Encontramos um número com vírgula como resposta e o resto zero.



33/2 = 16,5
 
33/2 = 16 + 1/2 (Deixamos o 1/2 porque não pudemos 1 dividir por 2, ou somente resto 1)

Pela equação da prova real:

16,5 x 2 + 0 = 33
16    x 2 + 1 = 33

Mas se não faz diferença a representação da resposta, porque existe duas formas diferentes?

Realmente na matemática não faz diferença, o grande detalhe está quando trazemos para a vida real.

Exemplo: Temos 33 pessoas em uma atividade e, queremos dividi-las em duplas (Ou seja, dividir por 2), não faz sentido dizer que vamos ter dezesseis grupos e meio. Afinal teríamos uma meia dupla, ou grupos com meia pessoa nele. 

Não tem como dividir uma pessoa ao meio, assim como não podemos dividir carros, animais, casas ... Então, nesses casos, usamos as respostas inteiras, terão 16 grupos e 1 pessoa sobrando, em outras palavras, ficando como resto.

Agora que sabemos que alguns números em divisões são fracionados, então como ficaria uma divisão por um número fracionado?

Vamos testar:

14 / 0,5

Agora precisaremos pensar, com muita atenção. Vamos fazer a tabuada de um número fracionado, podemos fazer mentalmente, ou escrito, depende da agilidade de quem estiver fazendo as contas:

0,5 x 1 =  0,5
0,5 x 2 =  1
0,5 x 3 =  1,5
0,5 x 4 =  2
0,5 x 5 =  2,5
0,5 x 6 =  3
0,5 x 7 =  3,5
0,5 x 8 =  4
0,5 x 9 =  4,5

*Não precisamos decorar todas as tabuadas que existem, até porque elas são infinitas, basta que façamos as tabuadas que precisamos na hora que precisarmos delas. Apenas pegue o número que desejado e multiplique por 1 até 9 e pronto, está feita.

Não encontramos um número que multiplicado por 0,5 é igual a 14. Então, teremos de fazer por partes. Sempre pegamos o primeiro elemento da esquerda do dividendo. Nesse caso o número 1. Sabemos pela tabuada que  0,5 x 2 = 1. Então, colocaremos 2 no resultado

Prosseguimos:

Agora que encontramos um zero, vamos para a outra parte:              

Percebam uma coisa interessante, ao dividir um número por uma fração, o resultado final é MAIOR que o número inicial. 

Veja pelo exemplo, 14/0,5 = 28. Ou seja, dividir por fração, resulta em um resultado maior que o número inicial, e essa mesma inversão acontece com multiplicação, multiplicar um número por fração, resulta em um número menor que o inicial.

Como faremos uma divisão com um dividendo terminando em zero?

Exemplo: 40/4

Inicialmente faremos igual qualquer outra vez. Pegaremos só o '4', do número 40, e faremos por parte:

Percebam que, encontramos um zero, ou seja terminamos com essa parte do número 40, mas a outra parte que está sobrando é também um 0.

Deveríamos continuar a conta, mas não podemos, afinal 00 é menor que 4. Então, nesse caso, coloca-se um zero no resultado e finaliza a divisão.

40 /4 = 10




Para finalizar, e se tivéssemos um número com um zero no meio?
Exemplo: 202 / 2

Faremos a divisão inicialmente normal, dividiremos o 202, agora em três partes, e começaremos à esquerda:

E então, encontramos um zero. Normalmente, iríamos para a próxima parte, ou seja, trazer mais um número para a conta, mas o próximo número é um zero. Basta, apenas, repetir igual antes, vamos colocar um zero no resto e um zero no resultado

Agora, continuamos, vamos para a próxima parte do número:

E seguimos até o fim da divisão:

Essa parte de divisões e multiplicações encerra aqui. Entretanto outras situações como dividir e multiplicar por 0 ou por 1, ou ainda o por que dividir por fração aumenta o resultado são abordadas em outra postagem mais detalhada. Clique aqui e depois aqui para continuar seu estudo.